Design of LOKI97

1. Design of LOKI97
   • Dr Lawrie Brown
     • Australian Defence Force Academy
2. Introduction
   • discuss design of LOKI97 cipher
   • new 128-bit private key block cipher
     • based on earlier LOKI89 & LOKI91
     • using latest cryptanalytic information
     • using extensive public cipher analysis
   • to be submitted to US NIST AES call
     • for new private key block cipher
     • stronger & faster than Triple-DES
3. Previous Work - LOKI89
   • 64-bit private key block cipher
   • Brown, Pieprzyk, Seberry 1989/90
     • see my PhD thesis
   • Biham & Shamir, Knudsen
     • diff crypt of reduced rounds
     • but full version secure
4. Previous Work - LOKI91
   • redesigned in 1991
     • by Brown, Kwan, Pieprzyk, Seberry
     • better round function & key schedule
   • Knudsen, Biham, Tokita et al
     • diff crypt of reduced rounds
     • linear crypt of reduced rounds
     • full version secure from DC & LC
     • some key schedule weaknesses
       • effective key size approx 60 bits
5. LOKI91 Overview
6. Why a New Cipher?
   • advances in computing hardware make exhaustive key search easier
     • cf. full 56-bit DES key broken
     • hence 64-bit key vulnerable soon
   • want much stronger key schedule
     • better immunity to related key attacks
   • US NIST AES call
7. Advanced Encryption Std
   • US NIST AES call for
     • private key symmetric block cipher
     • announced Sept 97, submit by Jun 98
     • 2 phases public evaluation, choose 1
   • requirements
     • 128-bit data, 128/192/256-bit keys
     • stronger & faster than Triple-DES
     • with full specification & design details
     • with both C & Java implementations
8. Cryptanalytic Advances
   • Differential Cryptanalysis
     • attack ciphers using relationships between pairs of encryptions with known input & observed output diffs
   • Linear Cryptanalysis
     • attack ciphers using (near) linear relationships between selected input, output, key bits
   • Related Key Attacks
     • attack using relations between keys
9. Design Considerations
   • Knudsen 93
     • no simple relations (vis data & key)
     • all keys are equally good
     • resistant to differential attacks
     • resistant to linear attacks
   • hence should have
     • non-linear key schedule
     • highly non-linear round function
     • efficient implementation with tables
10. LOKI97 Overview
    • LOKI97 is
      • private key feistel S-P block cipher
      • 128-bit data
      • 256-bit key schedule initialised from 128, 192, 256-bit keys
      • 16 round data computation using a complex highly non-linear function
        • two layers of designed S-P per round
      • same function also used in key schedule
11. LOKI97 Overview
    
12. LOKI97 Main Details
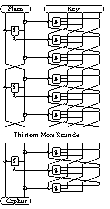
    • data computation
      • Ri = Li-1 xor f(Ri-1 + SK3i-2, SK3i-1)
      • Li = Ri-1 + SK3i-2 + SK3i
    • key schedule
      • SKi = K4i-1 xor f(K1i-1+K3i-1+nD, K2i-1)
      • K4i=K3i-1, K3i=K2i-1, K2i=K1i-1, K1i=SKi
      • D = (sqrt(5)-1).2⁶³
13. LOKI97 Round Function
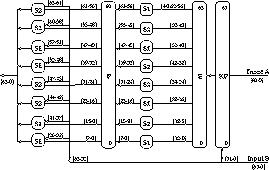
    • highly non-linear 64-bit function
      • f(A,B) = KP(Sb(P(Sa(E(A))),B),B)
    • 2 columns each of 2 S-boxes
      • Sa = [S2,S2,S1,S1,S2,S2,S1,S1]
      • Sb = [S1,S2,S1,S2,S2,S1,S2,S1]
    • regular perm P diffuses Sa outputs
      • fans S-box out to cover all Sb inputs
    • keyed permutation KP to exchange selected pairs of bits set by input B
14. LOKI97 Function f(A,B)
    
15. Rationale for S-boxes
    • Want S-boxes which must
      • be balanced
      • be highly non-linear
      • satisfy Strict Avalanche Criteria
      • have good XOR profile
    • cubing in odd Galois fields is good
      • S(x) = x³ mod p, p irred poly in GF2ⁿ
      • u used n=11 & 13
      • inverted input, truncated result to 8
16. Prelim Analysis: Key Sched
    • no general linear relations for keys
      • or keys with repeated subkeys, eg 0
    • can coerce first 4 subkeys to 0
      • by solving key schedule equations
        • SK1=0, K=[f(D,0)|0|0|0]
        • SK1,2=0, K= f(f(2D,0)+D,0)|f(2D,0)|0|0]
        • SK1,2,3=0, K=[f(f(f(3D,0)+2D,0)+D,f(3D,0))| f(f(3D,0)+2D,0)|f(3D,0)|0]
      • not a significant problem
17. Prelim Analysis: S-Boxes
    • XOR profiles very flat
      • S1 peak 64 (of 8192), zero peak 32
      • S2 peak 32 (of 2048), zero peak 16
      • ie std 2 round char has max Pr(1/256)
    • Avalanche
      • exhaustively tested all 1 bits changes
      • small number of 0 or 1 bit changes
        • similar to LOKI91
18. Prelim Analysis: Diff Crypt
    • mix of + and XOR hinders std DC
    • could consider "differences"
      • X' = [L1 xor L2, R1 - R2] BUT
      • keyed perm destroys arith diff
    • with std DC, have very small chance that XOR diff survives +
      • 2-round char, 0 out XOR, hits Sa only
      • actual char Pr << 1/256 due to use of +
      • any other char will involve both layers
19. Prelim Anal: Linear Crypt
    • can derive upper bounds from S
      • S1 approx Pr in ¹/2 +- 2^-7
      • S2 approx Pr in ¹/2 +- 2^-6
      • 1 round approx Pr in ¹/2 +- 2^-11
      • 16 round approx Pr in ¹/2 +- 2^-161
    • thus very unlikely to be significant
20. Prelim Analysis: Overall
    • early rand trials of 1-bit avalanche
      • showed almost exactly half output bits changing on a 1-bit input change
21. Conclusions
    • overview of LOKI97 design
      • previous work
      • rationale
      • goals
      • description
      • initial analysis
22. Further Information
    • on LOKI97
      • http://lpb.canb.auug.org.au/adfa/papers/ssp97
    • on AES
      • http://csrc.ncsl.nist.gov/encryption/aes/aes_home.htm
23. Questions

    ---

    Lawrie.Brown@adfa.edu.au / 05-May-98