Preliminary Thoughts on the Redesign of LOKI

DRAFT - 15 Dec 97

Dr Lawrie Brown

School of Computer Science, Australian Defence Force Academy, Canberra, Australia

Abstract

This paper sketches my thoughts on the redesign of the LOKI private key block cipher. My current tinman proposal is for a 16 round feistel cipher with 128-bit data and a 256-bit key schedule, which can be initialised by 128, 192, or 256-bit keys. The 16 rounds of the data computation use a balanced feistel network with a complex function f which incorporates two S-P layers. The 256-bit key schedule uses 33 rounds of an unbalanced feistel network using the same complex function f to generate the subkeys.

Introduction

LOKI91 is a 64-bit, 16 round, symmetric block cipher with a 64-bit user key. It was originally designed by L. Brown, J. Pieprzyk and J. Seberry in 1990 [BrPS90], and later re-designed (and renamed LOKI91), with improved resistance to differential cryptanalysis, by L. Brown, M. Kwan, J. Pieprzyk and J. Seberry [BKPS91].

The original version of LOKI89 was analysed by Biham and Shamir [BiSh91], and by Knudsen [Knud91]. They found that whilst reduced round versions of LOKI89 could be susceptible to differential cryptanalysis, the full 16 round version was not.

Following the redesign to LOKI91 to strengthen its immunity, it was analysed by Knudsen [Knud92]. He found that there was no characteristic with a probablility high enough to do a sucessful differential attack; that the size of the image of the F-function in LOKI91 is 8/13x2³²; and that there is a chosen plaintext attack that reduces an exhaustive key search on LOKI91 by almost a factor of 4 using 2³²+2 chosen plaintexts. In a subsequent paper, Knudsen [Knud94] discusses the concept of weak hash keys in LOKI.

Biham [Biha94c] introduced some new types of cryptanalytic attackes which exploit relations between sub-keys. He applied this attack to both versions of LOKI. For LOKI91 the complexity is of O(2⁶¹), which is faster than exhaustive search and comparable to Knudsen's results.

Tokita, Sorimachi, and Matsui [ToSM94] have examined the susceptibility of LOKI91 to linear cryptanalysis, and have found 12 or more round versions to be immune. Subsequently, Knudsen and Robshaw [KnRo96] have made incremental improvements to the search efficiency using non-linear approximations, but 12 or more rounds in LOKI91 is still immune. Recently Sakurai and Furuya [SaFu97] have described further incremental advances.

LOKI91 is currently regarded as a reasonably secure cipher, immune to both differential and linear cryptanalysis, whose main deficiencies are the linear key schedule which leaves it susceptible to some related key attacks, and the keysize which, given those attacks, is effectively about 2⁶⁰.

LOKI91 is described in Schneier [Schn96], which has led to some continued interest in its use by organisations wanted an unencumbered encryption algorithm. This is likely to continue with the release of a small, fast Java version in the publically available Cryptix library [Cryp97].

Redesign of LOKI

The main motiations for considering a further redesign of LOKI are the weaknesses caused by its key schedule, and the advances in computing hardware (as demonstrated by the recent brute force recovery of a 56-bit DES key [RSAD97]) which have rendered the keyspace too small. It is also an opportune time, given the currently open call for the submission of algorithms for the Advanced Encryption Standard [AES97].

In considering a redesign, I suggest there are a number of issues which need to be considered from both a security perspective, and from an implementation perspective.

Security Considerations

Knudsen [Knud93] specifies the following necessary conditions for a secure feistel cipher:

there are no simple relations
all keys are equally good
resistance to differential attacks
resistance to linear attacks

Based on these, the analyses of LOKI91 above, and comments on block cipher design in Schneier [Schn96], some issues I think need consideration from a security perspective include:

the key schedule needs to be non-linear in order to prevent the existance of equivalent keys, and related key attacks. Subkeys should be derived using a non-linear function (very likely the same one used in the data rounds), and subkey bits should depend on multiple key bits
the non-linear function should provide complete avalanche over all its bits in a single use
the non-linear function should be as immune as possible to differential or linear attacks
the non-linear function should be composed of a mesh of S-boxes with high non-linearity, with either a permutation or mixing operations used to provide avalanche
possibly making some component of the function dependent on key bits only (either some key only S-box inputs or a keyed permutation to selectively exchange bits)

Implementation Considerations

Issues for consideration from an implementation perspective include

S-boxes with around 12 input bits is about the largest practical for pre-computed table lookup, as a size tradeoff
S-boxes should ideally be functionally specified so the pre-computed tables can be constructed at run/instantiation time to minimise code size whilst maximising speed
the non-linear function should be computable with a small number of table lookups and other primitive operations

Lessons from Other Ciphers

In considering a redesign, I have looked for lessons to be learnt from ciphers which have been released subsequent to the design of the original LOKI. Descriptions of these ciphers have been taken from Schneier [Schn96] unless noted otherwise.

BLOWFISH: a 64-bit, 16 round feistel block cipher with a variable length key, designed by B. Schneier in 1994. It uses four large 8*32 bit random S-boxes generated from the supplied key, whose outputs are combined using addition and xor. This results in a fast cipher, provided the key is unchanged. The key schedule is long and complex. Vaudenay [Vaud96] has described attacks on reduced round versions, and noted some deficiencies caused by using sparse S-boxes.
CAST: a 64-bit, 8 round feistel block cipher with a 64-bit key, designed by C. Adams and S. Tavares in 1993. It uses six 8*32 bit S-boxes (some with data in, some with subkey in) whose outputs are combined using xor. These S-boxes are designed for and fixed per application. Vaudenay [Vaud96] also makes some comments on CAST and its use of sparse S-boxes, even though they are designed, not random.
ICE: a 64-bit, 16 round feistel block cipher with a 64-bit key (though other variants are also specified), designed by M. Kwan in 1997 [Kwan97]. It uses a keyed permutation along with fixed, highly non-linear S-boxes.
IDEA: a 64-bit, 8 round iterated block cipher with a 128-bit key, designed by X. Lai and J. Massey in 1990. It uses the concept of "mixing operations from different algebraic groups".
SAFER: a 64-bit, 6 or higher round, iterated block cipher with 64 or 128 bit keys, designed by J. Massey in 1994. It uses a round composed of a number of function layers, with 3 layers of PHT linear operations to promote avalanche. Analyses include Knudsen [Knud95] of a serious weakness in the original key schedule, and Knudsen and Berson [KnBe96] of a successive differential cryptanalysis attack on a 5 round version. They also note that the PHT transformation is the major source of weakness that permitted the attack.
SPEED: A variable data (64, 128 or 256), key (48-256) and round (>32) block cipher using an unbalanced feistel network, designed by Zheng in 1997 [Zhen97]. It uses a bitwise non-linear boolean operation and a data dependent cyclic shift in each round, with a large number of rounds needed given the simple round function, and the limited diffusion per round.
TEA: a simple 64-bit, 32 round feistel block cipher with a 128-bit key, designed by Wheeler & Needham [WhNe94] in 1994. It using a very simple round function composed of alternating additions and xor's along with left and right shifts, to provide non-linearity. This is iterated with a fairly high number of rounds to provide sufficient complexity.

Things of note:

random vs designed S-boxes: Schneier [Schn96] quoting L. O'Connor notes that for large S-boxes, using random boxes usually results in good choices. But there is also usually a fraction of bad boxes which can occur. I feel more comfortable with the idea of designed boxes with guaranteed characteristics. The disadvantage is that these are known and can be analysed (so we'd better get it right :-)
use of non-composable mixing operations: pioneered in IDEA, it has been used in a number of ciphers since. I think it is desirable to ensure that our round function utilises the concept that successive operations do not compose.
complexity of round function vs number of rounds: IDEA uses a more complex round function with a higher degree of security to use less rounds, whilst TEA illustrates the opposite approach. I'm inclined to the complex function approach.

The LOKI97 Proposal

LOKI97 is a 16 round Feistel cipher on 128-bit data using a complex non-linear function f(A,B), with a 256-bit key schedule which can be initialised using 128, 192, or 256-bit keys.

Data Computation

LOKI97 encrypts a 128-bit plaintext block to create a 128-bit ciphertext block. The data computation is initialised by dividing the 128-bit plaintext input value [L|R] into two 64-bit words:

      L₀ = L
      R₀ = R

These are then processed through 16 rounds (i=1,16) of a balanced feistel network:

      R_i = L_i-1 xor f(R_i-1+SK_3i-2,SK_3i-1)
      L_i = R_i-1+SK_3i-2+SK_3i

The resulting 128-bit ciphertext output value is composed of:

      [R₁₆|L₁₆]

after the final round, ie with no final swap as usual.

The function f(A,B) should be designed to ensure maximal avalanche between all input bits to the function. The current proposal for this function f(A,B) is given below.

Note the use of the "reversible" transformations (addition) on R as well as the more common transformation of L by XOR with the function output. This forms an incompatible group with the xor used on the previous round output, and hence provides some diffusion of the input bits into the function input, as well as obscuring the final input value.

The overall data computation thus looks as follows:

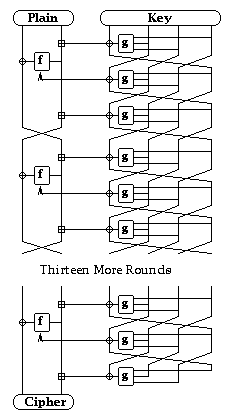
The decryption computation involves splitting the ciphertext

      L₁₆ = L
      R₁₆ = R

and then running the rounds in reverse. ie: use 16 rounds (i=16,1)

      R_i-1 = L_i xor f(R_i-SK_3i,SK_3i-1)
      L_i-1 = R_i-SK_3i-SK_3i-2

The 128-bit plaintext value is given by

      [R₀|L₀]

Key Schedule

LOKI97 uses a key schedule based on an unbalanced Feistel network (as per Schneier and Kelsey [ScKe96]), operating on four 64-bit words. It using the same function f(A,B) as the data computation to provide sufficient non-linearity to ensure that computing related keys is difficult.

The key schedule is initialised, based on the size of the key supplied, into the four 64-bit words [K4₀|K3₀|K2₀|K1₀] as follows:

Given a 256-bit key [K_a|K_b|K_c|K_d], let: [K4₀|K3₀|K2₀|K1₀] = [K_a|K_b|K_c|K_d]
Given a 192-bit key [K_a|K_b|K_c], let: [K4₀|K3₀|K2₀|K1₀] = [K_a|K_b|K_c|f(K_a,K_b)]
Given a 128-bit key [K_a|K_b], let: [K4₀|K3₀|K2₀|K1₀] = [K_a|K_b|f(K_b,K_a)|f(K_a,K_b)]

These are then processed through 48 rounds (i=1,48) to compute the 48 subkeys SK_i as follows:

      SK_i = K1_i = K4_i-1 xor g_i(K1_i-1,K3_i-1,K2_i-1)
      K4_i = K3_i-1
      K3_i = K2_i-1
      K2_i = K1_i-1

            where 

      g_i(K1,K3,K2)=f(K1+K3+(Delta*i),K2)

      Delta = (sqrt(5)-1)*2⁶³ = 9E3779B97F4A7C15₁₆

Three rounds of the key schedule are required to produce the three subkeys for each round of the data computation. Thus a total of 48 rounds are required for the key schedule, for a cost of approx three encryption computations.

The addition K1+K3+(Delta*i) forms an incompatible group with the xor used on the previous round output, as in the data computation. It includes multiples mod 2⁶⁴ of Delta, a value derived from the golden ratio, to reduce symmetry problems.

Decryption uses the keys in reverse order with (additive) inverses of the SK_3i-2 and SK_3i subkeys. These will need to be precomputed in encrypt order first - there is no reverse shortcut with this design.

Function f(A,B)

The highly non-linear function f(A,B) takes two 64-bit input values A and B, processes them using two layers of S-boxes with the highest possible non-linearity, to produce a 64-bit output. The two permutations are used to ensure maximal avalanche between all bits in the function.

The major novel feature in my proposed design is the use of two layers of the S-P network instead of just one, as in most other current feistel ciphers. This is to provide the desired maximal avalanche, as well as to minimise the posibility of suitable differential or linear characteristics. The presence of the keyed permutation on the input of the function, switching between different S-box inputs, ensures that predicting which S-box a particular input bit goes to is difficult. This increases the difficulty of deriving any useful attack characteristics.

This function is specified as follows:

      f(A,B) = Sb(P(Sa(E(KP(A,B)))),B)

Graphically, it looks as follows:

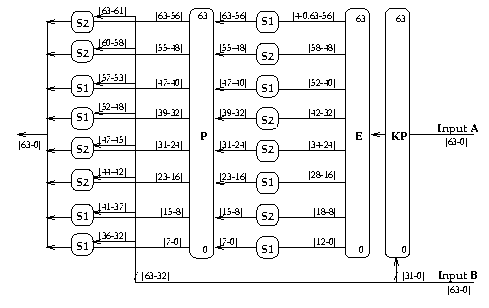
In more detail, the various component operations used are:

KP()
a very simple keyed permutation which splits its 64-bit input A into two 32-bit words, and uses the lower (rightmost) 32-bits of input B to decide whether to exchange corresponding pairs of bits in these words (if key bit is 1), or not (if key bit is 0), similar to that used in ICE [Kwan97]. It may be computed as:
KP([Al|Ar],SKr) = [((Al & ~SKr)|(Ar & SKr)) | ((Ar & ~SKr)|(Al & SKr))]
E()
expansion function, similar to LOKI91 but shifted for easier implementation, which selects overlapping groups of 13 bits (S1) or 11 bits (S2), so that at least some bits influence 2 S-boxes simultaneously, and with the preceeding addition, means all bits have some influence on multiple S-boxes. E thus maps a 64 bit input value [63-0] to a 96 bit output value [4-0,63-56|58-48|52-40|42-32|34-24|28-16|18-8|12-0].
Sa(), Sb()
are two columns of S-boxes, composed by concatenating boxes S1 and S2 (specified below), with Sa()=[S1,S2,S1,S2,S2,S1,S2,S1], and Sb()=[S2,S2,S1,S1,S2,S2,S1,S1]. In Sa() the inputs are autoclave (input+key from the output of E), in Sb() the upper bits are pure key bits (from the lower,rightmost 32-bits of B).
P()
permutation to diffuse S-Box outputs across full 64-bit width, using a regular, latin-square, pattern, similar to LOKI91, but with a slight change so the same output never goes to the corresponding input. P maps input bits [63-0] to
[56,48,40,32,24,16,08,00,57,49,41,33,25,17,09,01,
 58,50,42,34,26,18,10,02,59,51,43,35,27,19,11,03,
 60,52,44,36,28,20,12,04,61,53,45,37,29,21,13,05,
 62,54,46,38,30,22,14,06,63,55,47,39,31,23,15,07]

I believe this function should be implementable with 24 table lookups (8 each for Sa, P, and Sb), plus some and's, or's, xor's, shifts and adds for each round. This should make it reasonably fast and efficient to implement.

S-boxes

The S-boxes chosen for LOKI97 use cubing in an odd galois field GF(2ⁿ), as this has some highly desirable properties (such as maximal non-linearity, and a relatively flat XOR profile). In order to use odd inputs, S1 uses 13 input bits, and S2 uses 11. These are alternated as specified above to combine to work on an even input block. The input value is inverted (so that a 0 or 1 input does not give 0 or 1 output), and the output values are masked down to select the lower 8 output bits only. The S-box functions are thus:

      S1[x] = ((x xor 1FFF)³ mod 2911) & FF,  in GF(2¹³)

      S2[x] = ((x xor  7FF)³ mod  AA7) & FF,  in GF(2¹¹)

(nb. all constants above are written in hex, all computations are done as polynomials in GF(2ⁿ)

Certification Triples

A sample LOKI97 certification triple is:

LOKI97    key: 000102030405060708090A0B0C0D0E0F101112131415161718191A1B1C1D1E1F
LOKI97  plain: 000102030405060708090A0B0C0D0E0F
LOKI97 cipher: 75080E359F10FE640144B35C57128DAD

Arm Waving Cryptanalysis

My arm-waving quick glance cryptanal sez ...

key schedule: highly non-linear, sub-key bits are from output of function f(A,B) and depend in a complex way on all key bits. I can't see any obvious way of determining related keys, especially given the addition of the delta multiples in each round.
encryption computation: function f(A,B) is highly non-linear, has a strictly key dependent component, and has complete avalanche over the 64-bits of Input A, but partial avalanche only for input B, in one pass. It should be immune to both differential and linear cryptanalysis. There should be complete dependence on input and key after 3 rounds (nb. have incomplete dependence of L on L bits after first round).

For further work, should perhaps consider "differentials" where the L halves have a constant XOR whilst the R halves have a constant arithmetic distance. This will cancel the subkey on the first round, and allow comparisons of the round output, but only a 0 diff will have a chance of propogating to the next round. Also the final keyed permutation should pretty well destroy the probabilities.

Immediate Questions

At this early stage, the main questions I'd like opinions on are:

does the basic structure look reasonable?
do we have the right balance of complexity for data vs key schedule comps?
does the addition of multiples of delta mask symmetries in key sched sufficiently?
do we have the right number of rounds (rememebring the need for a sufficient margin of safety for the expected long cipher life)?

Conclusions

This paper includes my initial, preliminary, very tentative, early thoughts on redesigning LOKI.

Any or all of this is (and already has been) subject to complete revision, revolution or other changes beyond imagination!

Acknowledgements

The work was conducted during my special studies program in 1997, whilst visiting NTNU in Trondheim, Norway, and CCSR, UOW, Wollongong. I'd like to thank my colleagues at these institutions for their discussions and support.

References

AES97: "Advanced Encryption Standard Call", NIST, 1997. http://csrc.ncsl.nist.gov/encryption/aes/aes_home.htm.
BKPS91: Lawrence Brown, Matthew Kwan, Josef Pieprzyk, Jennifer Seberry, "Improving Resistance to Differential Cryptanalysis and the Redesign of LOKI", in Advances in Cryptology - Asiacrypt'91, Lecture Notes in Computer Science, Vol 739, Springer-Verlag, pp 36-50, 1991.
BiSh91: Eli Biham, Adi Shamir, "Differential Cryptanalysis Snefru, Kharfe, REDOC-II, LOKI and Lucifer", in Advances in Cryptology - Crypto'91, Lecture Notes in Computer Science, Vol 576, Springer-Verlag, pp 156-171, 1991.
Biha94c: Eli Biham, "New Types of Cryptanalytic Attacks Using Related Keys", Journal of Cryptology, Vol 7, No 4, pp 229-246, 1994.
BrPS90: Lawrence Brown, Josef Pieprzyk, Jennifer Seberry, "LOKI - A Cryptographic Primitive for Authentication and Secrecy Applications", in Advances in Cryptology: Auscrypt '90, Lecture Notes in Computer Science, Vol 453, Springer-Verlag, pp 229-236, 1990.
Cryp97: "Cryptix Java Cryptographic Library", 1997. http://www.systemics.com/docs/cryptix/.
KnBe96: Lars Knudsen, Thomas A. Berson, "Truncated Differentials of SAFER", in Fast Software Encryption 3, Lecture Notes in Computer Science, Vol 1039, Springer-Verlag, pp 15-26, 1996.
KnRo96: Lars Knudsen, M.J.B. Robshaw, "Non-linear Approximations in Linear Cryptanalysis", in Advances in Cryptology - Eurocrypt'96, Lecture Notes in Computer Science, Vol 1070, Springer-Verlag, pp 224-236, 1996.
Knud91: Lars Knudsen, "Cryptanalysis of LOKI", in Advances in Cryptology - Asiacrypt'91, Lecture Notes in Computer Science, Vol 739, Springer-Verlag, pp 22-35, 1991.
Knud92: Lars Knudsen, "Cryptanalysis of LOKI91", in Advances in Cryptology - Auscrypt'92, Lecture Notes in Computer Science, Vol 718, Springer-Verlag, pp 196-208, 1992.
Knud93: Lars Knudsen, "Practically Secure Feistel Ciphers", in Fast Software Encryption, Lecture Notes in Computer Science, Vol 809, Springer-Verlag, pp 211-221, 1993.
Knud94: Lars Knudsen, "New potentially "weak" keys for DES and LOKI", in Advances in Cryptology - Eurocrypt '94, Lecture Notes in Computer Science, Vol 950, Springer-Verlag, pp 419-424, 1994.
Knud95: Lars Knudsen, "A Key-Schedule Weakness in SAFER K-64", in Advances in Cryptology - Crypto'95, Lecture Notes in Computer Science, Vol 963, Springer-Verlag, pp 274-286, 1995.
Kwan97: Matthew Kwan, "The Design of the ICE Encryption Algorithm", in Fast Software Encryption 4, Springer-Verlag, 1997. http://www.cs.mu.oz.au/~mkwan/ice/paper.html.
RSAD97: "Government encryption standard DES takes a fall", RSA Data Security Inc, 1997. http://www.rsa.com/des/.
SaFu97: Kouichi Sakurai, Souichi Furuya, "Improving Linear Cryptanalysis of LOKI91 by Probabalistic Counting Method", in Fast Software Encryption 4, Springer-Verlag, 1997.
ScKe96: Bruce Schneier, John Kelsey, "Unbalanced Feistel Networks and Block Cipher Design", in Fast Software Encryption 3, Lecture Notes in Computer Science, Vol 1039, Springer-Verlag, pp 121-144, 1996.
Schn96: Bruce Schneier, "Applied Cryptography - Protocols, Algorithms and Source Code in C", 2nd edn, John Wiley and Sons, New York, 1996.
ToSM94: Toshio Tokita, Tohru Sorimachi, Mitsuru Matsui, "Linear cryptanalysis of LOKI and S2DES", in Advances in Cryptology - Asiacrypt '94,, Lecture Notes in Computer Science, Vol 917, Springer-Verlag, pp 293-306, 1994.
Vaud96: Serge Vaudenay, "On the Weak Keys of Blowfish", in Fast Software Encryption 3, Lecture Notes in Computer Science, Vol 1039, Springer-Verlag, pp 27-32, 1996.
WhNe94: David J. Wheeler, Roger M. Needham, "TEA, a Tiny Encryption Algorithm", in Fast Software Encryption 2, Lecture Notes in Computer Science, Vol 1008, Springer-Verlag, pp 363-366, 1994. http://www.cl.cam.ac.uk/ftp/papers/djw-rmn/djw-rmn-tea.html.
Zhen97: Yuliang Zheng, "The SPEED Cipher", in Financial Cryptography'97, BWI, Anquilla, pp 24-28, Feb 1997. http://pscit-www.fcit.monash.edu.au/~yuliang/pubs/speedc.tar.Z.

The latest version of this paper may be found at: http://lpb.canb.auug.org.au/adfa/papers/ssp97/loki97a.html.

Last updated: 15 Dec 97.