f(A,B),
with a 256-bit key schedule
which can be initialised using 128, 192, or 256-bit keys.
LOKI97 has evolved from the earlier LOKI89 [BrPS90], and LOKI91 [BKPS91] 64-bit block ciphers. Whilst LOKI91 is currently considered secure against known attacks such as differential and linear cryptanalysis, its effective key size of about 260 will be inadequate in future, as demonstrated by the recent brute force searches of 56-bit keyspaces [RSAD97]).
It was thus time to consider a redesign, which could address the deficiencies in the key schedule, and utilise a larger keyspace The currently open call for submission of candidate algorithms for an Advanced Encryption Standard [AES97] was a further inducement.
Consideration was given to the necessary conditions for a secure feistel cipher noted by Knudsen [Knud93]:
A number of other modern private-key block ciphers were reviewed in the early design phase, including Blowfish, CAST, ICE, IDEA, SAFER, SPEED and TEA (descriptions of most of which may be found in Schneier [Schn96]). A number of variant approaches were seen in these, including in the use of:
Also, to provide a stronger key schedule than previous LOKI variants, it was decided to use the same complex nonlinear round function in the key schedule, as in the data computation. This results in the computation cost of the key schedule being of the same order of magnitude as the data computation, that is not too costly for applications with periodic key changes, but costly enough to modestly penalise exhaustive key search operations which require a key change on each block.
In selecting suitable S-boxes, it was decided to select boolean
functions which are balanced, with the highest possible non-linearity,
satisfying the SAC criteria, and with a good XOR profile. Previous
experience has shown that such S-boxes result in designs resistant to
the known attacks (differential and linear cryptanalysis). Again the
results by Pieprzyk [Piep91] were used to select
appropriate functions. In particular he notes that cubing in odd-sized
galois fields GF(2n) are permutations with
maximal non-linearity. Each of the output boolean functions are
balanced, with maximum non-linearity, thus selecting only 8 (of the 11
or 13) still results in a function with the desired properties. The
high non-linearity implies that the SAC property holds, and subsequent
testing has shown these functions have a flat XOR profile, with peak
values only twice the average, and no peaks in the zero XOR column.
Pieprzyk has shown this is the expected profile for such functions.
Consequently these were chosen as the basis for the LOKI97 S-boxes.
[L|R] into two 64-bit words:
L0 = L
R0 = R
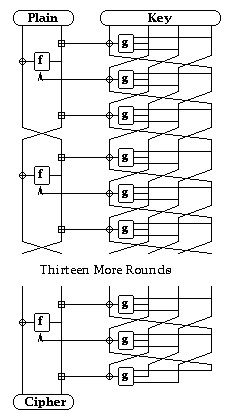
These are then processed through 16 rounds (i=1,16)
of a balanced feistel network:
Ri = Li-1 xor f(Ri-1+SK3i-2,SK3i-1)
Li = Ri-1+SK3i-2+SK3i
Each round uses both XOR (additional modulo 2) and integer addition (modulo
264) of the 64-bit data values. Since these are from incompatible
groups, the operations do not compose, and thus strengthen the rounds against
attacks, as well as obscuring the final round input value at the output, and
providing some additional diffusion of input bits.
The resulting 128-bit ciphertext output value is composed of:
[R16|L16]
after the final round, ie with no final swap as usual.
The function f(A,B) should be designed to ensure maximal
avalanche between all input bits to the function. The current proposal
for this function f(A,B) is given below.
The decryption computation involves splitting the ciphertext into two 64-bit words:
L16 = L
R16 = R
and then running the rounds in reverse. ie: use 16 rounds (i=16,1)
Ri-1 = Li xor f(Ri-SK3i,SK3i-1)
Li-1 = Ri-SK3i-SK3i-2
The 128-bit plaintext value is given by
[R0|L0]
The overall data computation thus looks as follows:

f(A,B) as the
data computation to provide sufficient non-linearity to ensure that
computing related keys is difficult.
The key schedule is initialised, based on the size of the key supplied,
into the four 64-bit words
[K40|K30|K20|K10]
as follows:
[Ka|Kb|Kc|Kd], let
[K40|K30|K20|K10] =
[Ka|Kb|Kc|Kd]
[Ka|Kb|Kc], let
[K40|K30|K20|K10] =
[Ka|Kb|Kc|f(Ka,Kb)]
[Ka|Kb], let
[K40|K30|K20|K10] =
[Ka|Kb|f(Kb,Ka)|f(Ka,Kb)]
These are then processed through 48 rounds (i=1,48) to compute
the 48 subkeys SKi as follows:
SKi = K1i = K4i-1 xor gi(K1i-1,K3i-1,K2i-1)
K4i = K3i-1
K3i = K2i-1
K2i = K1i-1
where
gi(K1,K3,K2)=f(K1+K3+(Delta*i),K2)
Delta = (sqrt(5)-1)*263 = 9E3779B97F4A7C1516
Three rounds of the key schedule are required to produce the three subkeys for each round of the data computation. Thus a total of 48 rounds are required for the key schedule, for a cost of approx three encryption computations.
The integer addition (module 264)
of K1+K3+(Delta*i) forms an incompatible
group with the xor used on the previous round output, as in the data
computation. It includes multiples mod 264 of
Delta, a value derived from the golden ratio, to reduce
symmetry problems.
Decryption uses the keys in reverse order with (additive)
inverses of the SK3i-2 and
SK3i subkeys.
These will need to be precomputed in encrypt order first - there
is no reverse shortcut as for LOKI89 and LOKI91.
f(A,B) takes two 64-bit
input values A and B, processes them using two layers of S-boxes with
the highest possible non-linearity, to produce a 64-bit output. The two
permutations are used to ensure maximal avalanche between all bits in
the function.
The major novel feature in my proposed design is the use of two layers of the S-P network instead of the one used in most other current feistel ciphers. This is to provide the desired maximal avalanche, as well as to minimise the posibility of suitable differential or linear characteristics. The presence of the keyed permutation on the input of the function, switching between different S-box inputs, ensures that predicting which S-box a particular input bit goes to is difficult. This increases the difficulty of deriving any useful attack characteristics.
This function is specified as follows:
f(A,B) = Sb(P(Sa(E(KP(A,B)))),B)
Graphically, it looks as follows:
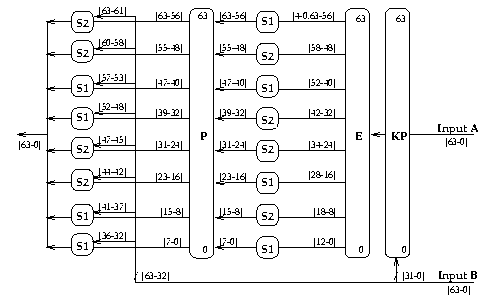
In more detail, the various component operations used are:
- KP()
- a very simple keyed permutation which splits its 64-bit input A into two 32-bit words, and uses the lower (rightmost) 32-bits of input B to decide whether to exchange corresponding pairs of bits in these words (if key bit is 1), or not (if key bit is 0), similar to that used in ICE [Kwan97]. It may be computed as:
KP([Al|Ar],SKr) = [((Al & ~SKr)|(Ar & SKr)) | ((Ar & ~SKr)|(Al & SKr))]- E()
- expansion function, similar to LOKI91 but shifted for easier implementation, which selects overlapping groups of 13 bits (S1) or 11 bits (S2), so that at least some bits influence 2 S-boxes simultaneously, and with the preceeding addition, means all bits have some influence on multiple S-boxes. E thus maps a 64 bit input value
[63-0]to a 96 bit output value[4-0,63-56|58-48|52-40|42-32|34-24|28-16|18-8|12-0].- Sa(), Sb()
- are two columns of S-boxes, composed by concatenating boxes S1 and S2 (specified below), with Sa()=[S1,S2,S1,S2,S2,S1,S2,S1], and Sb()=[S2,S2,S1,S1,S2,S2,S1,S1]. In Sa() the inputs are autoclave (input+key from the output of E), in Sb() the upper bits are pure key bits (from the lower,rightmost 32-bits of B).
- P()
- permutation to diffuse S-Box outputs across full 64-bit width, using a regular, latin-square, pattern, similar to LOKI91, but with a slight change so the same output never goes to the corresponding input. P maps input bits
[63-0]to[56,48,40,32,24,16,08,00,57,49,41,33,25,17,09,01, 58,50,42,34,26,18,10,02,59,51,43,35,27,19,11,03, 60,52,44,36,28,20,12,04,61,53,45,37,29,21,13,05, 62,54,46,38,30,22,14,06,63,55,47,39,31,23,15,07]
I believe this function should be implementable with 24 table lookups (8 each for Sa, P, and Sb), plus some and's, or's, xor's, shifts and adds for each round. This should make it reasonably fast and efficient to implement.
GF(2n), as this has some highly desirable
properties (such as maximal non-linearity [Piep91],
and a relatively flat XOR profile). In order to use odd inputs, S1 uses
13 input bits, and S2 uses 11. These are alternated as specified above
to combine to work on an even input block. The input value is inverted
(so that a 0 or 1 input does not give 0 or 1 output), and the output
values are masked down to select the lower 8 output bits only. The S-box
functions are thus:
S1[x] = ((x xor 1FFF)3 mod 2911) & FF, in GF(213)
S2[x] = ((x xor 7FF)3 mod AA7) & FF, in GF(211)
(nb. all constants above are written in hex, all computations are done
as polynomials in GF(2n)
A number of generators were trialed before the final selection of the ones specified above. All generators gave functions with maximal non-linearity, but there were small differences in other characteristics, such as variations in the avalanche characteristics. Those chosen resulted in a reasonable balance of the various measures tested.
LOKI97 key: 000102030405060708090A0B0C0D0E0F101112131415161718191A1B1C1D1E1F LOKI97 plain: 000102030405060708090A0B0C0D0E0F LOKI97 cipher: 75080E359F10FE640144B35C57128DAD